在木星繞太陽的軌道上, 有兩群小行星跟木星大約保持固定的距離, 一群領先木星 60度, 另外一群落後木星 60度, 兩群合稱為 Trojan asteroids 特洛伊小行星。 這兩個位置分別稱為 L4 與 L5, 是 「太陽-木星」 系統的五個 Lagrange points 拉格朗日點 其中之二。 L4 (L5 也一樣)、 太陽、 木星三者一直維持著正三角形的相對位置。
圍繞著共同質心旋轉的兩個較大星體 (例如太陽和木星)
對於第三個質量小到可以忽略的星體 (例如小行星) 會產生什麼樣的重力影響?
有沒有一些特殊的位置, 如果把小行星放在那裡,
它所受到的引力正好可以讓它跟木星同步旋轉太陽?
這個問題有五個解, 就稱為五個拉格朗日點。
駐點木星上的天文學家們, 從他們的角度來看,
這是五個幾乎不需要耗費能量的天然 停車場 停望遠鏡場。
事實上 韋伯望遠鏡和蓋亞望遠鏡就安置在 「太陽-地球」 系統的 L2 附近。
想要求拉格朗日點的座標, 比較簡單的方法是以太陽跟木星的質心為原點, 木星放在正 x 軸, 太陽放在負 x 軸, 以木星公轉軌道軸為 z 軸。 這個 「恆星行星旋轉系統」 (叫它 Srot 好了) 是一個旋轉而不是慣性的座標系 (叫它 S0 好了), 所以計算的時候需要加入離心力跟柯式力這兩個假想力。 詳見 旋轉參考系的假想力。
如果我們只關心相對於太陽與木星 靜止不動 的小行星, 那麼柯氏力為零, 小行星所受到的兩個萬有引力和一個離心力都是 conservative forces, 它們在空間中定義出三個 保守(力)場。 也就是說, 這幾個力場各自都可以寫成空間中某個純量數 (稱為該力場的位勢函數) 的梯度場。 參考 Dennis Westra 的講義 (原始網頁已消失)、 Neil J. Cornish 的文章、 Gary 的講義, 在 Srot 的 X-Y 平面上的一個位於 \( \mathbf{r} \) 處的單位質量的位能可以寫成: $$ - \frac{G M_s }{ | \mathbf{r}-\mathbf{r_s} | } - \frac{G M_p }{ | \mathbf{r}-\mathbf{r_p} | } + \frac{1}{2} \mathbf{\omega}^2 | \mathbf{r} |^2 $$ $$ = - \frac{G M_s }{ | \mathbf{r}-\mathbf{r_s} | } - \frac{G M_p }{ | \mathbf{r}-\mathbf{r_p} | } - \frac{G (M_s + M_p) |\mathbf{r}|^2 }{ 2 |\mathbf{r_s} - \mathbf{r_p}|^3} $$ 其中 \( M_s、 M_p、 \mathbf{r_s}、 \mathbf{r_p} \) 分別是恒星 (太陽) 與行星 (木星) 的質量和位置向量; \( \mathbf{\omega} \) 是 Srot 相對於 S0 旋轉角速度向量。 據此, 可以畫出 Srot 參考系的 X-Y 平面上的總位能場圖。
請下載 lagrange.gpt。
這是用 gnuplot
指令寫的小 script, 可以這樣執行: gnuplot lagrange.gpt
每按一次 enter 會畫下一張圖。 建議把繪圖視窗放到最大, 解析度高一點比較好看。
每一張圖其實都是俯視角度的立體圖; 可以用滑鼠旋轉, 看 3D 圖。
請忽略最開始的平面圖, 它的出現, 只是要讓你有放大圖形視窗的機會。
按 enter 之後, 接下來的圖分別是:
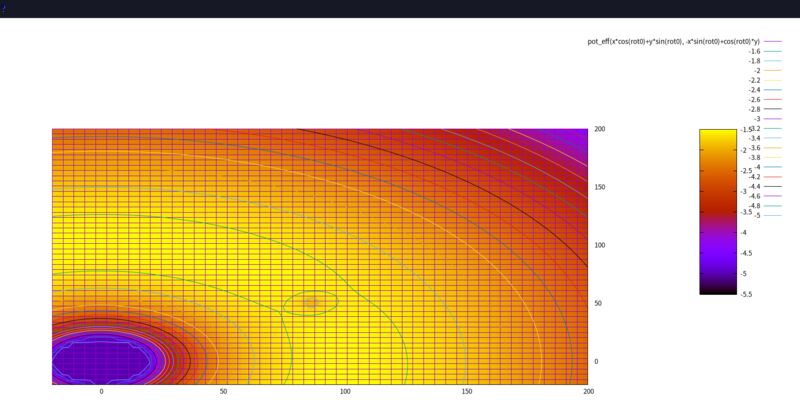
- 恒星-行星系統位能圖概觀
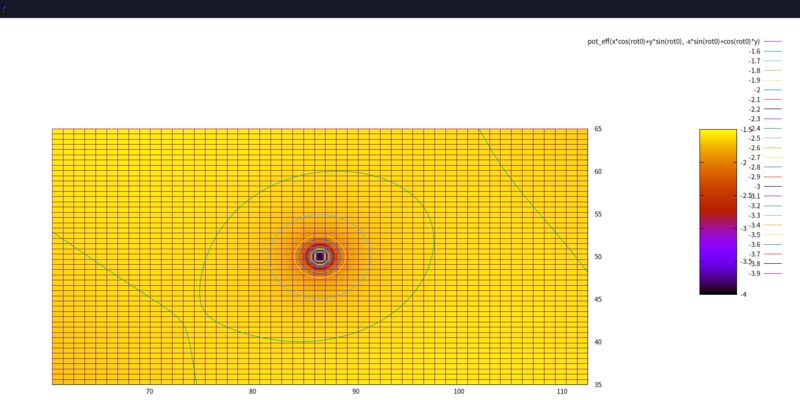
- 行星附近位能圖
- L1 附近
- L2 附近
- L3 附近
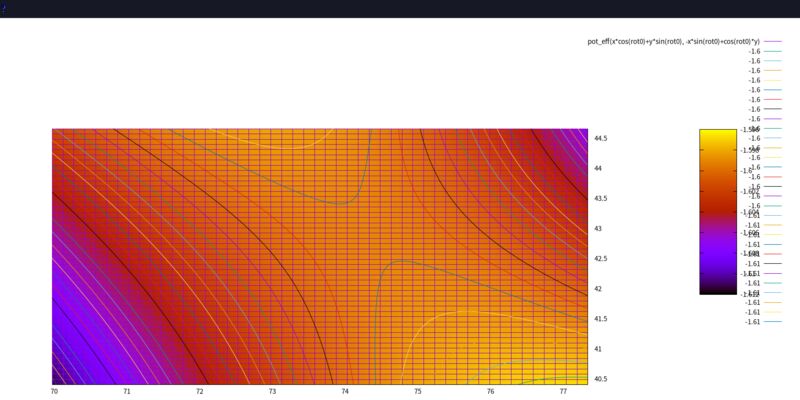
- L4 附近
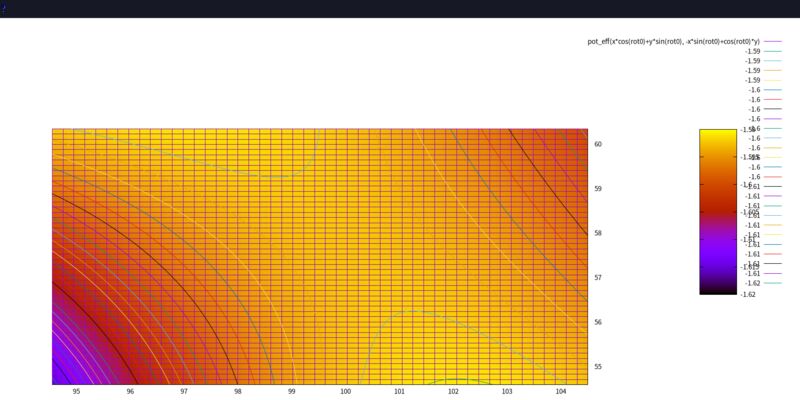
- L4 附近放大圖
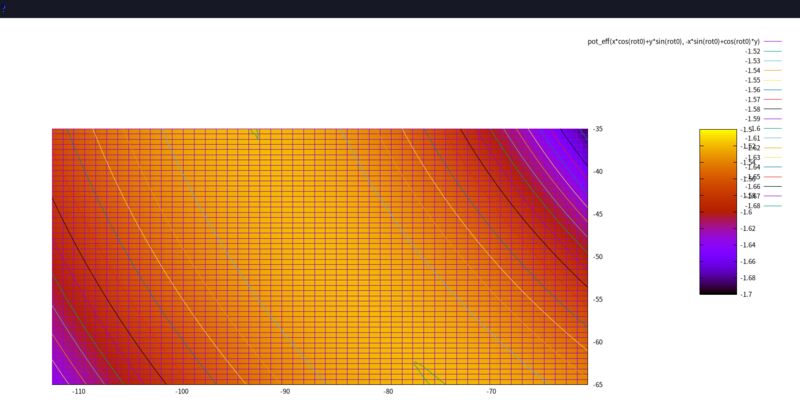
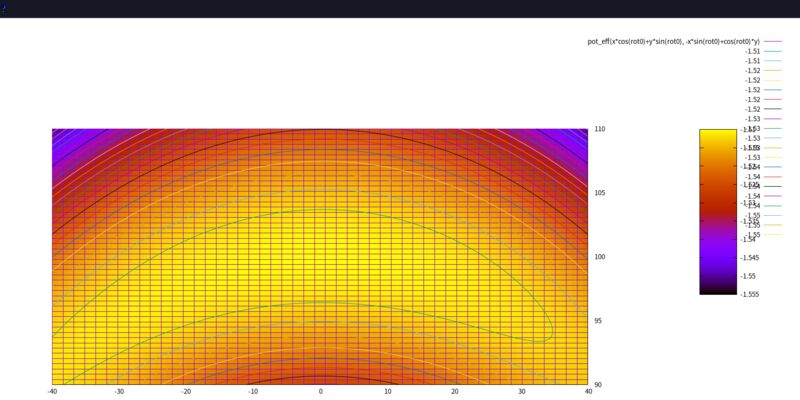
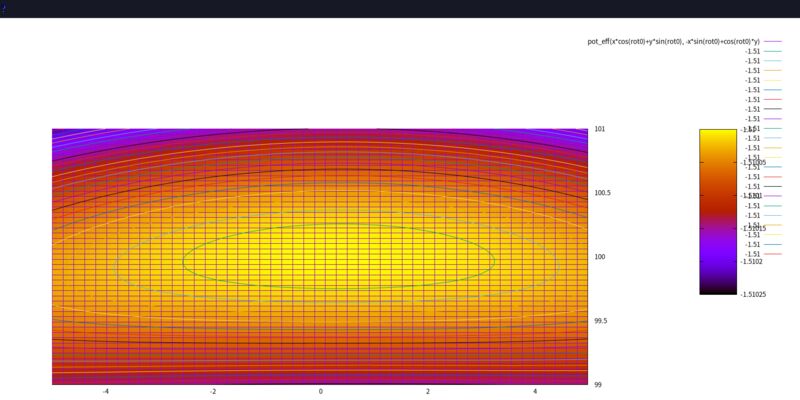
這個 script 畫圖的時候, 跟上面的解說有一些出入:
- 所有計算完成, 最後要畫圖之前, 旋轉了30度。 (
rot0 = pi/6) 所以行星以及 L1、L2、L3 的位置不在 gnuplot 的 X 軸, 而在 30度線上。 L4 正好跑到 90度的方向 (大約在 Y 軸上), 這樣放大 L4 附近的時候, 才比較容易看出它位於位能函數的極值附近。 (X 軸拉近較少, Y 軸拉近較多) - 離恒星或行星太近的 「位能深井」 被我填平了, 以免佔據太多等高線與顏色。
- 圖中行星的質量是恒星質量的 1%。 (Script 中的 alpha 值) 實際上木星的質量是太陽的 0.1%, 若以此比例畫, 在概觀圖上幾乎看不見。
拉格朗日點是位能函數的極值點, 可能是山頂、谷底或鞍點。 可以看到 L1、L2、L3 這三個點都是鞍點, 表示此處並不穩定, 稍微有點外力, 小行星就會掉出去。 而 L4... 竟是一個頂點? 極大值! 驚! 是我畫錯了嗎?
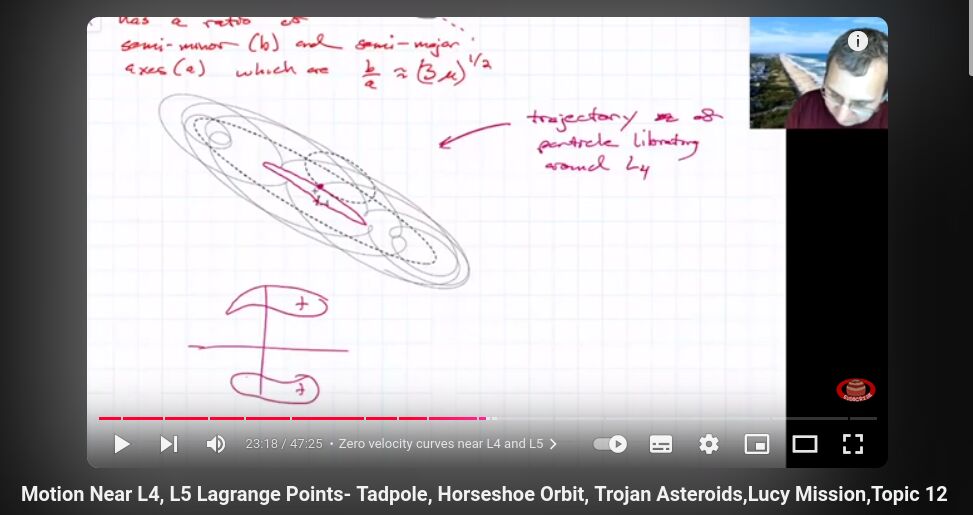 再次認真讀, 才發現 L4 是極大值沒錯。
但只要小行星一開始移動, 先前被我們忽略的柯氏力就會開始作用,
讓小行星圍繞著 L4 旋轉。 小行星的軌道並不是簡單的圓形或橢圓形,
而是一個快速旋轉的小圈繞著橢圓形的中圈旋轉,
中圈相對於 Srot 而言是靜止的;
但是從 S0 慣性座標系看,
這個橢圓形的中圈又繞著恆星行星系統質心旋轉。
天啊這也太花式了吧! 直接圖片搜尋 「tadpole orbit」 比較清楚。
大推 Ross 教授的影片,
省略數學式推導, 直接跳到結論: 20:00-30:30 及 41:00-44:45。
L4 附近的特洛伊小行星群聚成一坨類似蝌蚪的形狀, 所以統稱為 tadpole orbits。
有一些特洛伊小行星則是 (在 Srot 參考系裡面)
以近似馬蹄型的軌道在移動 (28:48) 所以稱為 horseshoe orbit。
從慣性參考系 S0 看則是: 當它快追趕上木星時就開始變慢;
當它快被木星追趕上時就開始變快。
這些奇怪的軌道, 感覺可以拿來寫科幻小說:
燃料不夠的時候從一顆小行星跳到另外一顆小行星之類的故事。
再次認真讀, 才發現 L4 是極大值沒錯。
但只要小行星一開始移動, 先前被我們忽略的柯氏力就會開始作用,
讓小行星圍繞著 L4 旋轉。 小行星的軌道並不是簡單的圓形或橢圓形,
而是一個快速旋轉的小圈繞著橢圓形的中圈旋轉,
中圈相對於 Srot 而言是靜止的;
但是從 S0 慣性座標系看,
這個橢圓形的中圈又繞著恆星行星系統質心旋轉。
天啊這也太花式了吧! 直接圖片搜尋 「tadpole orbit」 比較清楚。
大推 Ross 教授的影片,
省略數學式推導, 直接跳到結論: 20:00-30:30 及 41:00-44:45。
L4 附近的特洛伊小行星群聚成一坨類似蝌蚪的形狀, 所以統稱為 tadpole orbits。
有一些特洛伊小行星則是 (在 Srot 參考系裡面)
以近似馬蹄型的軌道在移動 (28:48) 所以稱為 horseshoe orbit。
從慣性參考系 S0 看則是: 當它快追趕上木星時就開始變慢;
當它快被木星追趕上時就開始變快。
這些奇怪的軌道, 感覺可以拿來寫科幻小說:
燃料不夠的時候從一顆小行星跳到另外一顆小行星之類的故事。
計算 L1、L2、L3 的時候, 假設了 Ms >> Mp, 因此如果 alpha 太大, 位置會不準確。 至於 L4 與 L5 的位置, 不論 alpha 大小, 都會落在正三角形的頂點; 但是如果 Ms < Mp*24.96, 這兩點就不再是穩定的位置。
 大人問小孩: 「全世界的玩具隨便你挑? 這怎麼可能?
如果我要的玩具只有一個, 正好又被別人借走了呢?」
大人問小孩: 「全世界的玩具隨便你挑? 這怎麼可能?
如果我要的玩具只有一個, 正好又被別人借走了呢?」


沒有留言:
張貼留言
因為垃圾留言太多,現在改為審核後才發佈,請耐心等候一兩天。