白話非對稱式密碼學 Asymmetric Cryptography

[2013/12/21 整個重新改寫][ sozi 簡報版]

什麼是 非對稱式密碼學 Asymmetric Cryptography 或 非對稱式加（解）密 Asymmetric Encryption（Decryption）？ 不必讀英文文章， 看 圖片搜尋結果 就可略知一二了。 右圖改編自 微軟官網。 先介紹一下術語。 如果甲（左側 sender）想寄私密訊息給乙（右側 recipient）， 他可以用一把金鑰 （key） 對明文 （plaintext， 就是未加密的原始訊息） 進行 加密 （encrypt）， 產生 密文 （cyphertext）。 如果他們所採用的加解密演算法 夠好的話， 密文根本就是一堆亂碼， 就算貼在網頁上昭告天下也沒關係， 因為沒有人看得懂。 乙收到密文之後， 再用金鑰對密文進行 解密 （decrypt）， 又得到明文。

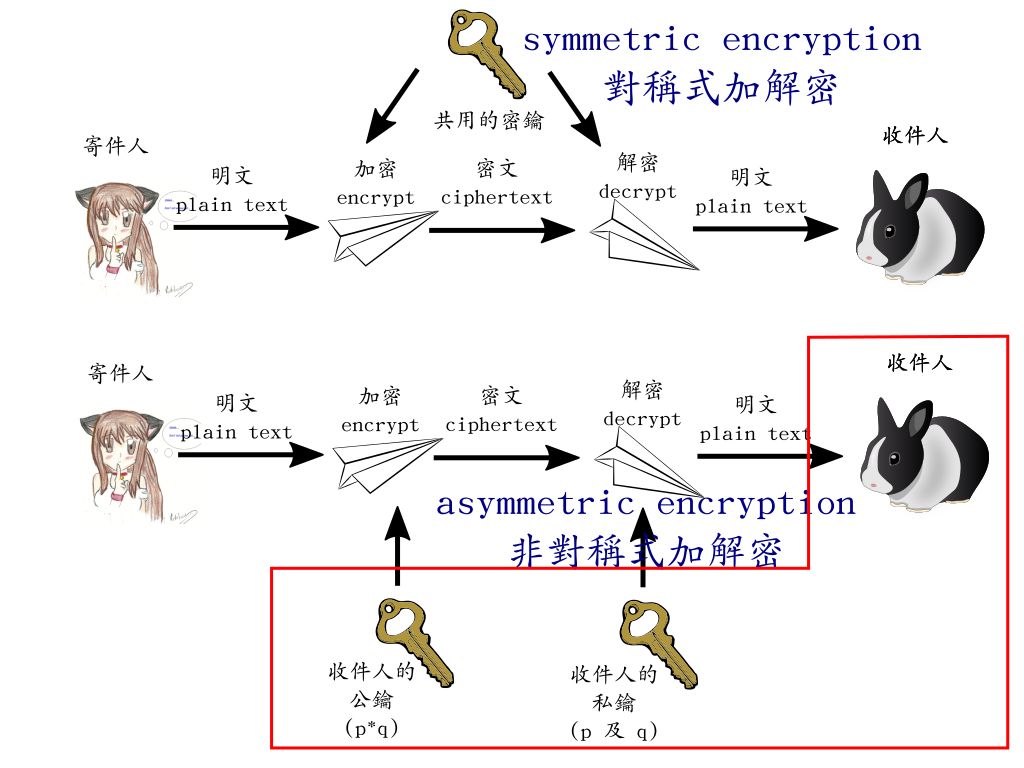
比較古老的方法， 加密跟解密用的是同一支金鑰， 稱為 「對稱式加解密 symmetric encryption/decryption」， 如圖上半所示。 今日的通訊軟體， 加密跟解密時， 用的則是成對產生的兩支不同金鑰， 這類演算法稱為 「非對稱式加解密 asymmetric encryption/decryption」， 如圖下半所示。 這兩枝金鑰一枝稱為公鑰 （public key）， 通常會在網站上昭告天下； 另一枝稱為私鑰 （private key）， 是持有人自己小心保護、 不讓任何人看到的秘密。 右圖特別值得注意的是： 加密時， 採用 收件人的公鑰； 解密時， 採用 收件人的私鑰。

[本段可略過] 加密演算法所運用的概念其實很簡單： 找一個很 "困難"、 連全世界最聰明的數學家都只能用笨笨的方法算到地老天荒的問題， 把它反轉過來， 就變成了保護秘密的工具。 例如非對稱式密碼學領域裡， 最容易理解的 「困難」 問題， 就是因數分解。 沒錯， 國中生就懂的這個題目， 就算丟給頂尖的數學家去解， 他們的解法也比窮舉法好不到哪裡去。 所以如果你能把加密演算法設計成 「破解它跟做因數分解一樣曠日費時」， 那麼它就是一個基本的非對稱式密碼學演算法了。 如果說丟出來挑戰竊聽者的問題等同於 「分解 r = p*q 」， 那麼你可以想像： 收件人的公鑰裡面就含有等同於 r 的資訊； 而收件人的私鑰裡面則含有等同於 p 跟 q 的資訊。 更精確的定義請見 RSA basics 或 How RSA Works With Examples。 因為這些數字超大 (多達2048甚至4096bits) ， 不可能用人工方式產生、 記憶， 所以保護私鑰的方式， 通常是用一個用戶自選的 passphrase 把它上鎖。 而產生公鑰私鑰時， 當然也不可能人工手選質數， 所以需要用到 亂數產生器 random number generator。 也因此， 如果亂數產生器被動手腳 (例如 NSA 要求微軟支援的 Dual EC DRBG) 那麼非對稱式加解密的保護力就會破功。 例如 Dual EC DRBG 所產生的是藏有後門的金鑰， 從公鑰就可以推出私鑰。

比方說你 （sender 甲） 有重大的內幕消息要爆料給貴哥知道， 但是擔心貴哥 （recipient 乙） 的 e-mail 被黃世銘檢查總長監看。 於是你在 MIT 的 PGP Key Server 搜尋到幾年前貴哥自己貼上去的公鑰。 你把 [貴哥的公鑰] 跟 [內幕消息] 餵給加密軟體 gpg 吃， 於是產生一堆亂碼 （密文）。 你可以很放心地把這堆亂碼 e-mail 給貴哥， 甚至就算直接把這堆亂碼以匿名的方式貼在貴哥的部落格也沒問題， 因為只有貴哥的私鑰能夠解密 （把 cipher text 轉成 plain text）， 所以只有貴哥可以解讀你的內幕消息； 其他人 -- 就算是無法無天無所不能的黃世銘 -- 即使看見留言內容也完全不知道你在說些什麼。

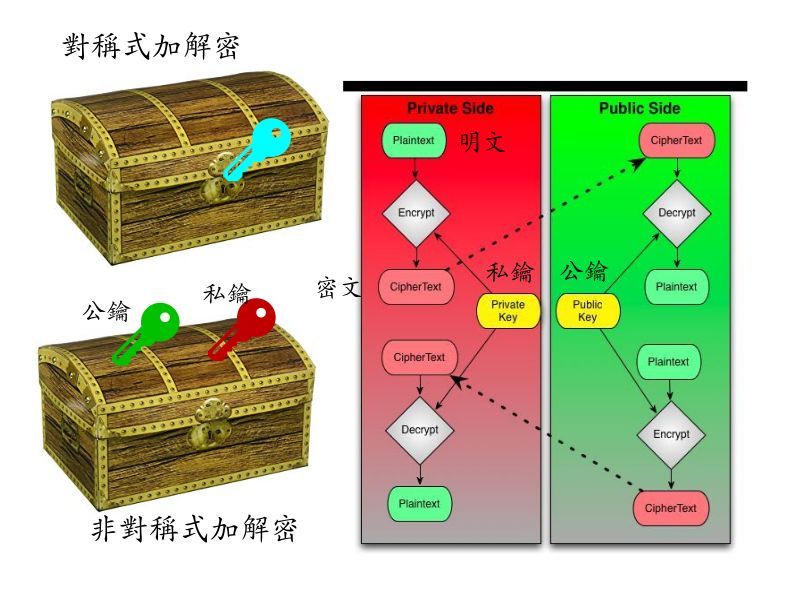右圖的右半出自 ScienceBlogs， 作者 Mark C. Chu-Carroll。 上一段的解釋， 對應到這張圖的右下 （加密過程） 與左下 （解密過程）。 [2021/7/23] 下圖解釋真正的 end-to-end encryption (e2ee)， 這種設計是不可能有 Man-in-the-Middle attack (中間人攻擊) 。 然後你就理解為什麼我說 (允許中間人攻擊的) iMessage 根本就是一種後門設計。

[2019/3/25 重寫數位簽章的說明] 事實上， 非對稱式密碼學演算法所產生出來的公鑰私鑰還有另一個用途： 它可以拿來做 數位簽章 （digital signature）， 也就是 Mark Chu-Carroll 的圖的上半部所描述的狀況。 在一筆比特幣交易當中， 如果 A 要付款給 B， 可能會有一段類似這樣的訊息： 「本人同意從 (我持有的) X 位址支付若干比特幣給 Y 位址」。 當然， 這必須加上 A 的數位簽章才有公信力。 這時 A 就拿他的私鑰 (付款人的私鑰) 對上述訊息加密 （圖的左上）， 得到的看似亂碼的 cipher text 就是數位簽章。 任何人都可以拿 A 的公鑰 (付款人的公鑰) 去對這數位簽章解密， 把看似亂碼的 cipher text 解碼成為原來承諾文的明文 plain text。 （圖的右上） 這裡的重點其實並不是要保護那一段文字， 而是要向世界證明寫那段明文的是 A 本人無誤。 因為除了 A 本人之外， 沒有人能用那把獨一無二的 private key 寫出這種 「跟 A 的 public key 匹配的 亂碼文章」。 以上就是 「數位簽章」 的核心原理； 這也是為什麼區塊鏈的每一筆交易記錄裡要包含付款人的公鑰、 為什麼我們說每一個 (由某公鑰所產生的) 位址都被 (對應的) 私鑰所保護。 也請參考 兩把刷子程度的 密碼貨幣與區塊鏈。

順便一提， cryptocurrency 應該稱為「密碼貨幣」而不是「加密貨幣」， 因為它用到密碼學當中的 單向雜湊函數 以及非對稱式密碼學的「數位簽章」部分， 但並沒有用到「加解密」的部分。 如果你公開募款， 那麼任何人都可以在區塊鏈探索工具上面看到該位址的所有交易歷史記錄， 完全沒有秘密可言。

嗯， 最早， 寫這帖的原因是為了要寫 螢幕廣播工具 iTALC 教學； 最近重新改寫， 則是因為今年六月以來， 從 美國 NSA 無所不在的監聽 到臺灣行政院的 「行動裝置安全謊言」 以及 蘋果電腦 iOS7 的 MDM 監聽陰謀 讓大眾感受到保護自身隱私的重要性， 所以打算寫更多加密相關的教學文， 又把這篇翻出來修改。 員工如果擔心自己的電腦/平板/手機被公司監聽， 固然可以根據 個人資料保護法 主張自己的隱私； 但與其事後靠法律彌補， 不如事前用技術預防。 而加密就是最好的自保方式， 所以加解密的基本原理， 應該是現代公民必備的基本常識。