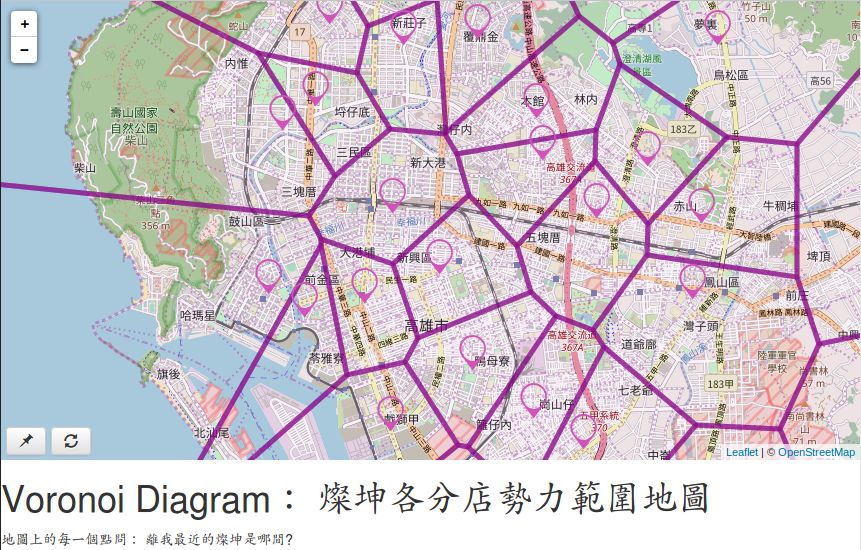
用 GRASS 繪製燦坤各分店的勢力範圍地圖 Voronoi Diagram

想像你有一張 「中華電信基地臺分佈地圖」， 並且假設每個基地臺的功率都一樣大。 地圖上的每一個點都可以問： 「哪一個基地臺離我最近?」 以便決定哪個基地臺的訊號比較強、 我的手機要跟誰連線。 以 (不會移動的) 「偶像 - 粉絲」 之間的關係來比喻， 每個偶像有自己的勢力範圍， 範圍內的所有點就是它的粉絲。 各勢力範圍之間的分界線由相鄰兩偶像的垂直平分線所組成。 這樣畫出來的圖稱為 Voronoi Diagram。 因為我拿不到基地臺座標， 所以只好改畫燦坤各分店的勢力範圍地圖。 目前可能沒什麼用， 因為分店跟粉絲的直線距離沒有太大意義； 但以後出現無人機送/取貨業務時， 這張地圖可能就有用了。

位於最外圍的偶像， 它的勢力範圍會延伸到無窮遠， 也就是說地圖上會有一些無窮大的區塊。

把相鄰的兩座偶像用一條 edge 連起來， 這樣畫出來的圖 (也就是 Voronoi Diagram 的 dual graph) 稱為 Delaunay Triangulation。 這個圖有一些特性：

1. 它的最外圍就是所有偶像的 convex hull。
2. 這些偶像之間的 nearest neighbor graph 是它的子圖。 (問每一個偶像： 除了你自己之外， 誰是你的偶像?)
3. 在所有的 triangulations 當中， 它所畫出來的三角形最胖。 (它的最小角比別種 triangulation 的最小角要大)。

我唸博士班時的專長就是計算幾何。 可惜這領域在臺灣沒有很紅， 我也沒有勇氣當先鋒， 所以後來就沒再玩了。 對理論有興趣的讀者， 可以讀臺師大資工系的 演算法筆記。 在 「Computational Geometry」 段落裡面有很多篇計算幾何相關的連結。 (點進去就有中文了。)

下面談實作。 平面上給定 N 個點， 計算 Voronoi Diagram 要花 O(N log N) 的時間。 從它算出 Delaunay Triangulation (或是反過來) 只需要 O(N) 的時間。 最受歡迎的實作是 qhull， 它平時花 O(N log N) 的時間； 不過 詳細的分析 有點複雜。 qhull 超強的地方在於 (1) 它能處理高維空間中的點 (2) 它能處理三點共線、 四點共面等等類型的問題 (這比前者更困難許多)。 例如 python 的 scipy.spatial.Voronoi 底下的引擎採用的就是 qhull。

但其實你連 python 程式都不必寫。 假設你已經 用 GRASS 建了一個測試用的 mapset， 就可以拿 grass 來找出一堆點的 Voronoi Diagram 跟 Delaunay Triangulation。 GRASS 的版本也很強， 它還可以計算區域 (而不是只限點) 的 Voronoi Diagram 。

請下載 tkec.tgz。 它裡面的 *.html 檔案是從 這裡 抓來的。 經過這樣的處理： for f in *.html ; do extract.php -s 'table:nth-of-type(3) td' < $f | perl -pe 's/\n//g' | perl -pe 's#<td[^>]*>([^<>]*店)</td>#\n$1#g; s#</td>##g; s#<.*?>#,#g' ; echo ; done | grep -v '名稱.*電話' | perl -pe 's/號.*?(樓|F|B1)$/號/ ; s/(\.|、)\d+//g ; s/,\d+號/號/ ; s/(號)+/號/' > tkec.csv 產生了 tkec.csv。 如果想要了解細節， 建議先把 do ... done 中間那一段複製出來、 只作用在一個 html 檔上面， 逐步看它的輸出。 再用手工整理 「大坪林店 198200號」、 「後龍店 及205號」、 「鳳山店 7,8號」、 「鹽埕店 110&112號」、 「羅東中正」 等等錯誤或特殊列， 並且餵給 李小淮大大的線上地址轉經緯度， 或是 TGOS 全國門牌地址定位服務， 最後就產生壓縮檔裡面的 tkec-coords.csv。

再來用 GRASS 進入你的實驗用 mapset (圖集)， 然後：

v.in.ascii input=/路徑/tkec-coords.csv output=tkec separator=',' x=5 y=4
v.delaunay input=tkec output=tkecdt
# g.region -pa vect=tkec res=1
g.region w=116E e=124E n=28N s=20N
v.voronoi input=tkec output=tkecv

v.out.ogr input=tkecdt output=tkec-dt.geojson format=GeoJSON
v.out.ogr input=tkecv output=tkec-vor.geojson format=GeoJSON

第一句話讀入 tkec-coords.csv 檔， 並且在 GRASS 裡面建立 tkec 這張地圖。 第二句話計算 Delaunay Triangulation、 產生一張名為 tkecdt。的新地圖。 第四句話類似， 但產生名為 tkecv 的 Voronoi Diagram 地圖。 不過在計算 Voronoi Diagram 之前， 必須先用 g.region 指令設定計算範圍。 (兩句 g.region ... 擇一即可。) 在 GRASS 裡面， g.region 通常是給 raster map 用的； vector map 的運算通常不需要設定 g.region。 不過因為 Voronoi Diagram 會畫出無窮的區域， 所以需要先用 g.region 對運算範圍設限。 最後兩句話把算出來的兩張圖匯出成 .geojson 檔。 然後就可以拿去 potluckmap 畫出 燦坤各分店勢力範圍地圖 (我只放了 Voronoi Diagram， 沒有放 Delaunay Triangulation， 以免畫面太亂)。 從這個圖好像可以大約看出人口分佈耶!

順便介紹 grass 命令列上的幾個常用指令：

1. g.mapset -l 列出目前的 project 裡， 有哪些 mapset 可用； g.mapset -p 現在正在使用哪個 mapset 。
2. g.list type=all 列出目前的 mapset 裡面的所有地圖。
3. v.info map=tkec 查詢 tkec 這張地圖的摘要資訊。
4. v.db.select map=tkec | less 列出 tkec 這張地圖內所有元素的屬性資料， 並且用 less 逐頁查看。
5. g.remove -f type=vector name=tkecv 刪除 tkecv 這張地圖。
6. man g.list 查看 g.list 如何使用。

注意到在 grass 裡面也可以使用 pipe 呼叫 shell 裡面的指令 (例如第三句的 less)， 很方便。