透過 maxima 感受「平方反比定律」 的神奇

忘記很久以前在哪裡讀到， 說 萬有引力的平方反比定律 裡面這個 "2" 次方是很神奇、 很剛好的數字。 也忘記到底是怎麼剛好法。 最近心血來潮， 開始讀 向量場的數學， 在 Anchordoqui 寫的講義 裡面讀到一個範例 (5.3 節範例 3)： 令 r=(x,y,z) 表示空間中一個起始於原點的向量。 如果向量場 vf3 的數學式是： vf3(r) = r/|r|^3， 那麼 vf3 的散度 (divergence) 到處都是零。 讀者不用擔心高深的數學， 這裡我只假設讀者知道純量場、 向量場跟偏導數的定義。 至於一個向量場 vf3 的散度， 它只不過是一個 公式很簡單的純量場。 至於它有什麼物理意義或數學特性， 就暫時先隨便無所謂了。

如果以某個大質量物體 (例如太陽) 的中心作為座標軸的原點， 那麼在空間中某個點 r=(x,y,z) 所感受到的重力向量的值就是： -r/|r|^3 跟上面的式子只差一個負號。 所以我很自然地想問： 如果是 r/|r|^2 這樣的向量場， 它的散度的公式會很複雜嗎? 那 r/|r|^4 這個向量場呢?

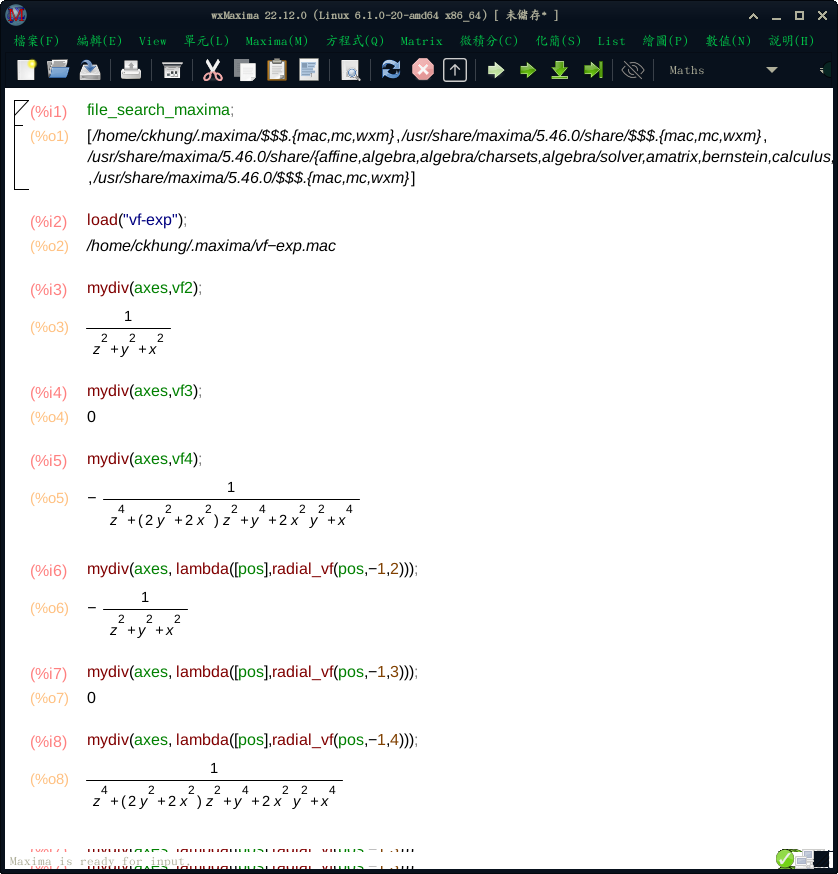
要叫我手工計算也是可以啦， 但比起花二十分鐘做無聊的運算， 我更願意藉這個動機花一天學 (好久以前就想學的) 符號運算軟體 maxima。 它有兩個不同版本的圖形介面： wxmaxima 跟 xmaxima。 看完 這則討論， 決定貼 wxmaxima 的截圖給大家看。 但不知為何我的 wxmaxima 一直閃個不停， 而且是白底視窗。 還是回到黑底綠字文字視窗裡面使用原始、陽春的文字介面， 我比較習慣。

我們先定義 (由 a、 b 兩個參數所 "點名" 的) 一大家子的函數 (a family of functions)： radial_vf(pos, a, b) := a*pos/(pos.pos)^(b/2); 這裡的 pos 是一個三維向量， 而 . 則是向量的內積， 所以 (pos.pos)^(1/2) 就是向量的長度 (pos 與原點的距離) 。 其中我們真正有興趣的是 radial_vf([x,y,z], 1, 3)， 也就是 Anchordoqui 講義裡面所舉的範例 3， 還有 radial_vf([x,y,z], -1, 3) 也就是重力向量場。 我們也想知道其他不同乘方 (不同 b 值) 的向量場的 div 公式會不會很複雜。

再來是定義 divergence operator。 先用這個版本除錯： one_third_div(vf, axes):=block([],print(vf(axes)[1], axes[1]),diff(vf(axes)[1],axes[1])); 它只計算三項當中的一項， 但是寫成 block 的形式， 所以可以加上 print 指令方便查看參數的值。 成功之後用 sum 函數創造迴圈並且把三項加總起來， 最後再用 ratsimp 簡化分式， 就完成了： mydiv(vf, axes) := ratsimp(sum(diff(vf(axes)[i],axes[i]), i, 1, 3));

使用的時候可以先鎖定 a,b 這兩個參數， 抓出一大家子當中的某個函數： vf2(pos):=radial_vf(pos,1,2); 定義好 vf2 再拿它來當參數： one_third_div(vf2, axes); 或 mydiv(vf2, axes); 。 也可以拿 (用丟即棄的) lambda expression 直接呼叫： mydiv(lambda([pos],radial_vf(pos,1,2)), axes);。 改變 a 的值， 只有常數倍的影響 (其實 grad、 div、 curl 都具有 linearity 的特性)； 改變 b 的值則可以看出： 唯有平方反比定律的式子 (b=3) 會很神奇地讓散度變成四處皆零。 小時候的好奇心終於得到了一小部分的滿足!

可以把 完整的程式碼 放到 ~/.maxima/ 底下， 然後用 load("vf-exp"); 載入。 如果將來事業做很大， 想要另外建一個 maxima 專用的函式庫目錄， 也可以 在 file_search_maxima 變數後面 append 你自己的函式庫目錄。 程式看起來很短， 但其實我除錯很久才寫出來， 主要是因為一開始搞不太清楚該如何把函數當成參數來傳， 進到函數裡面以後不知道該如何呼叫它，而且還不知道該如何除錯。 最終是 這個解答 拯救了我。 另外， subst 好像也可以解決我的問題。 很後來才發現已經有人寫好 現成的 grad、 div、 curl。 這些連結暫時沒用到， 先筆記一下就好。

除了單老師的中文 maxima 講義之外， 英文的 maxima by example 跟 maxima tutorial 看起來也很棒。 不過好玩的東西太多了， 所以一如往常， 沒定性的我， 學會一兩招解決眼前的問題， 就收工暫時把玩具丟在一旁， 以後不知道什麼時候才會再有需要回來 maxima 學更多...